Implement Heap Sort using C++

A heap is a tree-based data structure in which the tree is almost a complete binary tree. The maximum number of a child node in a binary heap is at most 2.

Implement a Heap Sort Function using C++

In a binary heap, the height of a heap tree is log2N if the heap is a complete binary tree of N nodes.

If a complete binary tree with n nodes is represented using an array, then for any node with index I, 1<=i<=n, we can access the nodes using the following formulas.

Max-heap is a property of heap that ensures that for every node i, other than the root,
Array [Parent of i node] >= A[i]

In a max-heap, the root always contains the largest element. In a min-heap, the condition is reversed and the root always contains the smallest element.

Let’s say, we have a heap with elements stored in an array called arr. To convert this array into a heap, access the node in the array. Then, check if its left and right sub-trees are max heaps and if the node itself contains the largest value than all of the child nodes.

Heapsort runs in two phases. In the first phase, we build a heap, and in the second, we translate it into a sorted list by maintaining the max-heap property.

Implementation of max-heapify is as follows

void maxHeapify(int n, int i) {
    int large = i,
         left = 2 * i + 1,
         right = 2 * i + 2;
    if (left < n && arr[left] > arr[large])
        large = left;
    if (right < n && arr[right] > arr[large])
        large = right;
    if (large != i) {
        t = arr[i];
        arr[i] = arr[large];
        arr[large] = t;
        maxHeapify(n, large);
    }
}

The logic is simple.

The function takes two parameters: an array, and an index of the node(i) that needs to be heapify.

Initially, we store i in the variable called largest.

Implementing the above logic using C++

void maxHeapify(int n, int i) {
  int large = i,
    left = 2 * i + 1,
    right = 2 * i + 2;
  if (left < n && arr[left] > arr[large])
    large = left;
  if (right < n && arr[right] > arr[large])
    large = right;
  if (large != i) {
    t = arr[i];
    arr[i] = arr[large];
    arr[large] = t;
    maxHeapify(n, large);
  }
}

Heap sort routine code

void heap_sort() {
    for (int i = n / 2 - 1; i >= 0; i--)
        maxHeapify(n, i);
    for (int i = n - 1; i >= 0; i--) {
        t = arr[0];
        arr[0] = arr[i];
        arr[i] = t;
        maxHeapify(i, 0); 
    }
}

Now the above from the main method:

#include <iostream>
#include<conio.h>
#include<stdlib.h>

using namespace std;
void heap_sort();
void maxHeapify(int, int);

int   t, a;
int n =5;
int arr[5] = {3,4,1,7,5};

int main() {
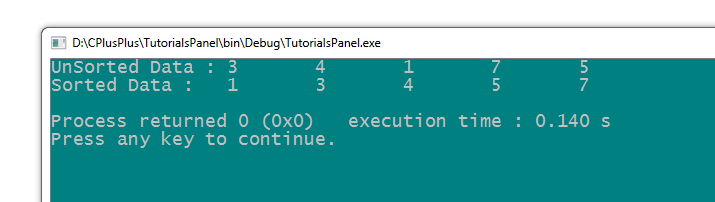
    cout << "UnSorted Data :";
    for (int i = 0; i < n; i++) {
        cout << "\t" << arr[i];
    }
    heap_sort();
    cout <<endl<< "Sorted Data :";
    for (int i = 0; i < n; i++) {
        cout << "\t" << arr[i];
    }
    cout<<endl;
    return 0;
}

Related Articles